词法分析 | RE 转化成 NFA Thompson 算法

Thompson 算法

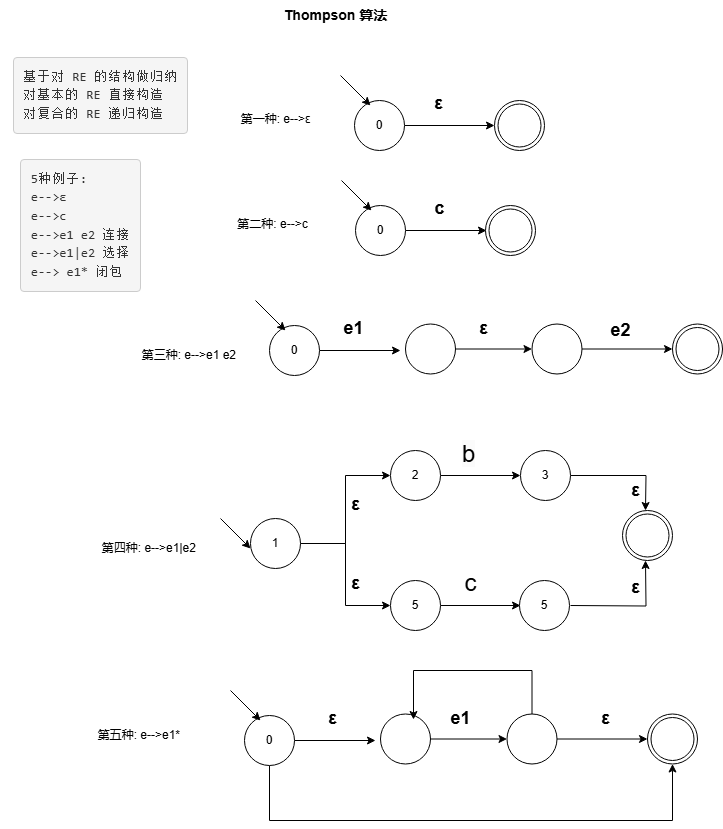
基于对 RE 的结构做归纳
对基本的 RE 直接构造
对复合的 RE 递归构造

如图。举例出5种方式

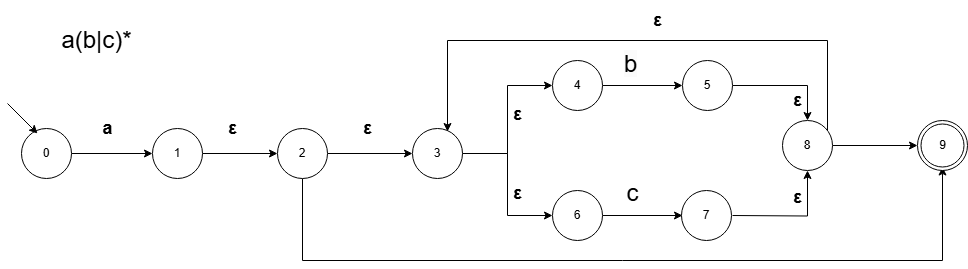
如a(b|c)*  这样的怎么构造呢？

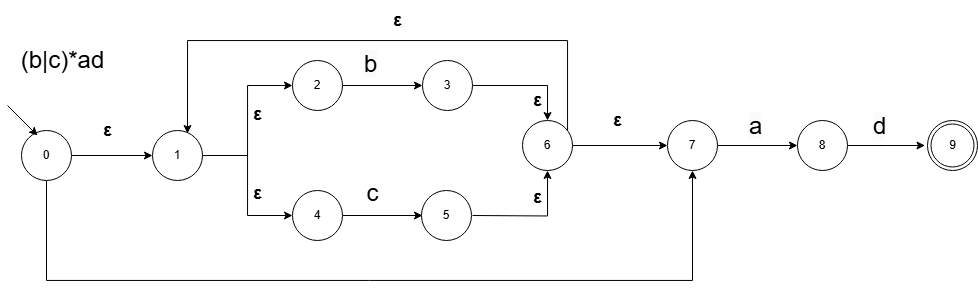
(b|c)*ad

使用代码实现a(b|c)*   实现

#状态类
class State:
    def __init__(self, is_accepting=False):
        #接受状态
        self.is_accepting = is_accepting
        self.transitions = {}

    def add_transition(self, input_symbol, target_state):
        self.transitions[input_symbol] = target_state

    def __str__(self):
        return f"State {id(self)}: Accepting={self.is_accepting}"

class NFA:
    def __init__(self):
        self.states = []
        self.start_state = None
        self.accept_states = []

    def add_state(self, state):
        self.states.append(state)

    def set_start_state(self, state):
        self.start_state = state

    def set_accept_state(self, state):
        self.accept_states.append(state)

    def add_epsilon_transition(self, from_state, to_state):
        from_state.add_transition(None, to_state)

    def add_symbol_transition(self, from_state, input_symbol, to_state):
        from_state.add_transition(input_symbol, to_state)

    def __str__(self):
        return "\n".join(str(state) for state in self.states)

    def accepts(self, input_string):
        current_states = [self.start_state]
        for char in input_string:
            new_states = []
            for state in current_states:
                for symbol, target_state in state.transitions.items():
                    if symbol is None or symbol == char:
                        new_states.append(target_state)
            if not new_states:
                return False
            current_states = new_states
        return any(state.is_accepting for state in current_states)

# 创建NFA
nfa = NFA()

# 创建状态
state0 = State()
state1 = State(is_accepting=True)

# 添加状态到NFA
nfa.add_state(state0)
nfa.add_state(state1)

# 设置开始和接受状态
nfa.set_start_state(state0)
nfa.set_accept_state(state1)

# 添加转换
nfa.add_symbol_transition(state0, 'a', state1)  # a -> state1
nfa.add_symbol_transition(state1, 'b', state1)  # b -> state1
nfa.add_symbol_transition(state1, 'c', state1)  # c -> state1
nfa.add_epsilon_transition(state1, state1)     # ε -> state1

# 测试NFA
input_string = "abbbbbb"
if nfa.accepts(input_string):
    print(f"The NFA accepts the input string '{input_string}'")
else:
    print(f"The NFA does not accept the input string '{input_string}'")