词法分析 | DFA 的最小化

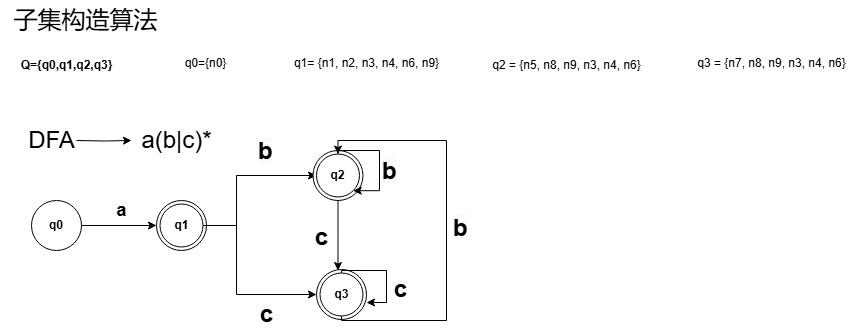
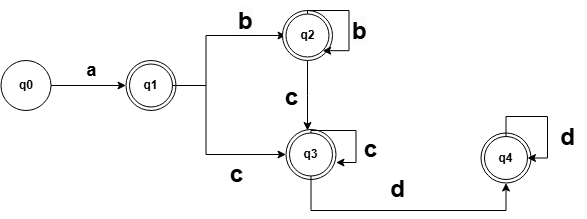
还是已获得的a(b|c)* 为例子

已经获取到了这样一个的DFA的。这样的一个DFA可以通过Hopcroft 算法得到更为简单的一个DFA

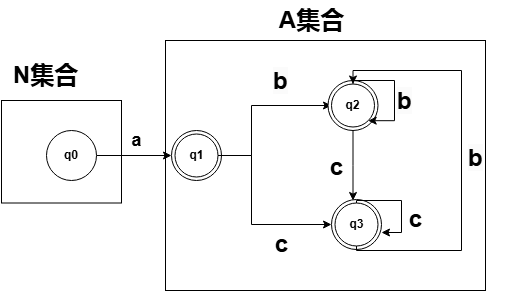
Hopcroft 算法初始化N 和A

A 代表是终态集合 就是接受集合

N 代表非终态集合 没有接受的集合

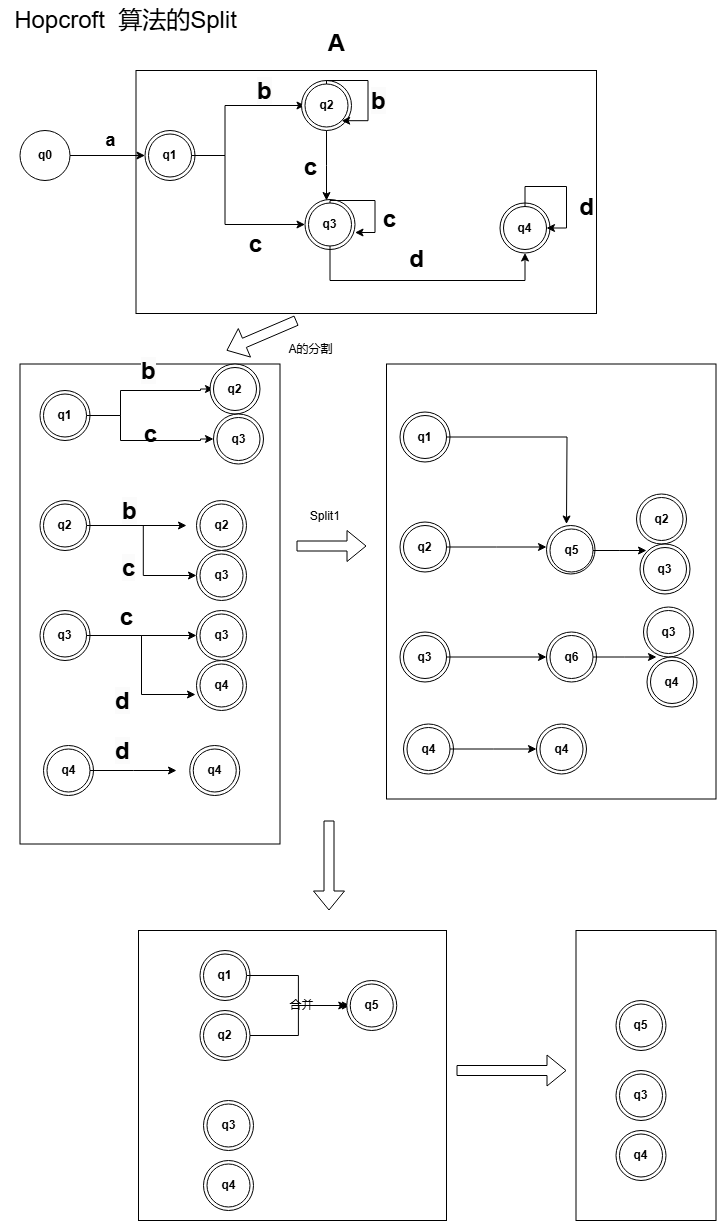
画个图可以更好的理解

使用切分集合的方式进行最小化。例如上图的N 里面只有一个元素了。就没有办法分割了。

那么就可以分割A

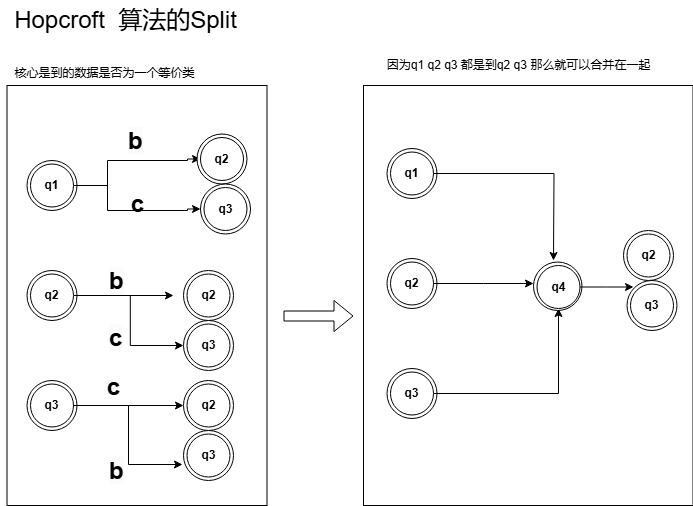
那么A通过怎么样子的进行分割呢？

通过等价类是否一致的话。进行分割。如图

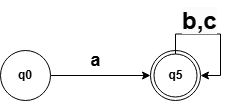
因为q1 q2 q3 都是到了一个q4 等价类那么就可以合并成一个q5 如下：

如果q1 q2 q3 指向不一样的情况下怎么分割呢？例如下图

这里q3 输入d 指向了q4 那么就变成了如下

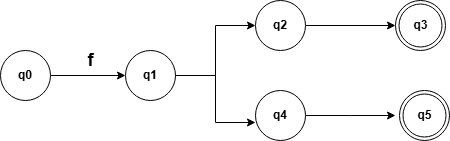
例子2 :f(ee|ie)

N : {q0, q1, q2, q4}

A : {q3, q5}

在 N 中 q0 和 q1 在接受 e 的条件下最终得到的状态还是在 N 的内部。所以可以将其根据 e 拆分成 {q0, q1}, {q2, q4}, {q3, q5}

对于 q2 和 q4 都可以接受 e ，而且最终达到的状态一致，所以不能再进行切分。

q0 和 q1 ，在接受 e 的时候， q0 最终得到还是在 {q0, q1}这个状态的结合中， q1 却会落在 {q2, q4} 的状态中，所以可以将 q0 和 q1 分为 {q0}, {q1}。