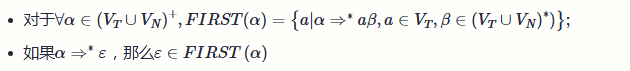词法分析 |LL(1) 文法

作者: print("") 分类: 编译原理 发布时间: 2025-01-05 00:43

一、LL(1) 文法介绍
第一个L代表 分析时从左向右扫描
第二个L代表分析过程将最左推导 

1 代表只需要向右看一个符号

二、NULLABLE 集合

nullable 介绍

非终结符 X 属于集合 NULLABLE，当且仅当：

基本情况：X -> ε
归纳情况：X -> Y1 … YnY1, … , Yn 是 n 个非终结符，且都属于 NULLABLE 集

所以，对于如下给出的两个例子，都不属于 NULLABLE：

  1. X -> a
  2. X -> β1 … βn。 βi 是终结符，但是存在一个 βj 可以推出 a。（推出结果中必定存在一个字符）

伪代码 

NULLABLE = {};
while (nullable is still changing)
    foreach (production p: X -> β)
        if (β == ε)
            NULLABLE U= {X}
        if (β == Y1 ... Yn)     // 非终结符
            if (Y1 ∈ NULLABLE && ... && Yn ∈ NULLABLE)
                NULLABLE U= {X}

对于给定的产生式规则如下所示，其分析表得到如下：  

Z -> d
   | X Y Z
Y -> c
   |
X -> Y
   | a
NULLABLE 0 1 2
{} {Y,X} {Y,X}

第一次循环得到了{Y,X}  因为和第0次循环的结果发生了变化触发了第二次循环。第二次循环还是{Y,X} 就得到了{Y,X}

三、FIRST 集合

FIRST(N) = 从非终结符N开始推导的出句子开头的所有可能终结符号集合

公式：

简单理解为:就是找终结符
 

对 N-> a ....
FIRST(N) U ={a}  

如果把a换成一个变量M  M代表终结符例如a 或者b 或者 c 或者n
对 N-> M ....
FIRST(N) U ={M}

一个简单的例子 

例如
S -> N 
N --> A C
A -->| b 
C --> a 
那么FIRST(A)={b,a}

3.1 FIRST不动点算法

FIRST 集合的完整计算公式 

基本情况
X -> a
FIRST(X) U= {a}
归纳情况
X -> Y1 ... Yn
FIRST(X) U= FIRST(Y1)
if Y1 ∈ NULLABLE, FIRST(X) U= FIRST(Y2)
if Y1, Y2 ∈ NULLABLE, FIRST(X) U= FIRST(Y3)
......

FIRST 集的完整不动点算法

foreach (nonterminal N)
    FIRST(N) = {}

while (some set is changing)
    foreach (production p: N -> β1 ... βn)
       foreach (βi from β1 upto βn) 
            if (β1 == a ...)   // 最右推导  β1
                FIRST(N) U= {a}
                break
            if (β1 == M ...)
                FIRST(N) U= FIRST(M)
                if(M is not in NULLABLE)
                    break

对于给定的产生式规则如下所示，其分析表得到如下：  

Z -> d
   | X Y Z
Y -> c
   |
X -> Y
   | a

得到如下的FIRST分析表

N\FIRST 0 1 2
Z {} {d} {a,c,d}
Y {} {c} {c}
X {} {c,a} {c,a}

五、FOLLOW集合

FOLLOW 集合的定义

对于一个非终结符 A，FOLLOW(A) 定义为可能在任何句型中紧跟着 A 出现的终结符的集合。如果 A 是某个句型的最右符号，则将结束符 $（或 #）加入 FOLLOW(A)。

计算 FOLLOW 集合的步骤：

对于文法的开始符号 S： 将 $ 加入 FOLLOW(S)。这是因为分析过程总是从开始符号开始，并以 $ 结束。

1、对于文法的开始符号 S： 将 $ 加入 FOLLOW(S)。这是因为分析过程总是从开始符号开始，并以 $ 结束

2.、对于产生式 A -> αBβ

    将 FIRST(β) – {ε} 加入 FOLLOW(B)。也就是说，如果 B 后面跟着 β，那么 β 的 FIRST 集合中除了 ε 之外的所有终结符都可能紧跟着 B

    如果 ε ∈ FIRST(β)，或者 β 是空串，则将 FOLLOW(A) 加入 FOLLOW(B)。也就是说，如果 B 后面的符号可以为空，那么任何可以跟在 A 后面的符号也都可以跟在 B 后面。

通过例子详细说明： 

S -> A B
A -> a | ε
B -> b | ε

计算过程 

1. FOLLOW(S) 由于 S 是开始符号,将 $ 加入 FOLLOW(S) 因此，FOLLOW(S) = {$}。 
2. FOLLOW(A)：A 出现在产生式 S -> A B 中。 
	将 FIRST(B) - {ε} 加入 FOLLOW(A)。FIRST(B) = {b, ε}
	所以 FIRST(B) - {ε} = {b}。因此，将 b 加入 FOLLOW(A)
	由于 ε ∈ FIRST(B)，根据规则 2 的第二部分，
	将 FOLLOW(S) 加入 FOLLOW(A)。FOLLOW(S) = {$}。
	因此，FOLLOW(A) = {b, $}。 
3.  FOLLOW(B):根据规则 2, B 出现在产生式 S -> A B 中。
	由于 B 是产生式的最右符号（β 是空串），
	根据规则 2 的第二部分，将 FOLLOW(S) 加入 FOLLOW(B)。
	FOLLOW(S) = {$}。因此，FOLLOW(B) = {$}

FOLLOW(S) = {$}
FOLLOW(A) = {b, $} 
FOLLOW(B) = {$}

FOLLOW 集的不动点算法

foreach (nonterminal N)
    FOLLOW(N) = {}
while (some set is changing)
    foreach (production p: N -> β1 ... βn)
        temp = FOLLOW(N)     // temp 记录在 βn 的后面
        foreach (βi from βn downto β1)   // 逆序 !!! 逆序的 FOLLOW。
            if(βi == a...)  // terminal 
                temp = {a}
            if (βi == M ...)    // nonterminal 
                FOLLOW(M) U= temp
                if(M is not NULLABLE)
                    temp = FIRST(M)
                else temp U= FIRST(M)

对于给定的产生式规则如下所示，其分析表得到如下：  

Z -> d
   | X Y Z
Y -> c
   |
X -> Y
   | a

得到如下的分析表

N\FOLLOW 0 1 2
Z {} {} {}
Y {} {a,c,d} {a,c,d}
X {} {a,c,d} {a,c,d}

六、SELECT集合

SELECT 集合的定义

对于一个产生式 A → α，其 SELECT 集合定义为：在输入流的当前符号为 a 的情况下，如果 a 属于 SELECT(A → α)，那么可以选择该产生式进行推导。

更具体地，SELECT 集合的定义分为两种情况：

  1. 如果 α 不能推导出 ε（空串）： SELECT(A → α) = FIRST(α)。也就是说，如果 α 不能推导出空串，那么其 SELECT 集合就是 α 的 FIRST 集合。

  2. 如果 α 可以推导出 ε（空串）： SELECT(A → α) = (FIRST(α) – {ε}) ∪ FOLLOW(A)。也就是说，如果 α 可以推导出空串，那么其 SELECT 集合是 α 的 FIRST 集合（去除 ε）和 A 的 FOLLOW 集合的并集。

伪代码 

foreach (production p)
    FIRST_S(p) = {}
calculte_FIRST_S (production p: N -> β1 ... βn)
    foreach (βi from β1 to βn)
        if(βi == a...)  // terminal 
            FIRST_S(p) U= {a}
            return;
        if (βi == M ...)    // nonterminal  
            FIRST_S(p) U= FIRST(M)
                if(M is not NULLABLE)
                    return;
    FIRST_S(p) U= FOLLOW(N)

如上我们已经有了三个集合、整理到一起

NULLABLE={X,Y}

X Y Z
FIRST {a,c} {c} {a,c,d}
FOLLOW {a,c,d} {a,c,d} {}

根据伪代码可以计算出SELECT 集合如下

0 1 2 3 4 5
SELECT {d} {a,c,d} {c} {a,c,d} {a,c,d} {a}


七、LL(1)表

0: Z -> d
1:   | X Y Z
2: Y -> c
3:   |
4: X -> Y
5:   | a

根据上述已经完成的SELECT 集合可以构造出LL(1) 表

a c d
Z 1 1 0,1
Y 3 2,3 3
X 4,5 4 4

转成成文法的LL(1)表

a c d
Z Z->X Y Z Z->X Y Z Z-d,Z->X Y Z
Y Y-ε Y->c,Y-ε Y-ε
X X->Y,X-a X->Y X->Y



八、LL(1)表冲突

如上Z,d 值中的0,1   和Y,c 的值2,3  X,a 值是 4,5  这就出现了冲突。可以通过消除左递归的方式进行解决冲突

一、消除左递归

例如：一个文法如下

0:  E -> E+ T
1:       |  T
2:  T -> T *F 
3:       |  F
4:   F -> n

我们构造出来的LL(1)表会如下

n + *
E 0,1
T 2,3
F 4

主要的原因是由于存在左递归、使得0条语句和第1条语句存在交集、第2条语句和第3条语句存在交集

那么就需要去掉交集、例如 

0:  E -> E+ T
1:       |  T

他的交集是T+T+T+T+T+T+T+T+T+T+T    这种方式 那么可以把第一个T提取出来

构造如下的 

0:  E -> T E'
1:  E' -> T E'
2:       |

通过这样的方式就可以消除交集、生成新的规则

0:  E -> T E'
1:  E' -> T E'
2:       | 
3:  T ->  F T'
4:  T' -> * F T'
5:        |
6:  F -> n

那么构造出新的LL(1) 表如下

n + *
E 0
E’ 1
T 3
T’ 5 4
F 6

那么通过消除左递归后就发现表中是没有冲突的。

二、提取左公因子

 例如如下的文法 

0: X -> a Y
1:      | a Z
2: Y -> b
3: Z -> c

主要是思想是把相同的进行合并例如 第0 行和1 行都出现了a 那么可以把a 提取出来。然后Y  Z 合并  如下

0:  X ->  a X'
1:  X' -> Y 
2:       |  Z

九、练习1 

1: lexp -> atom | list
2: atom -> number | identifier
3: list -> (lexp-seq)
4: lexp-seq -> lexp-seq lexp | lexp

要求 

(a) Remove the left recursion
(b) Construct the First and Follow set of the nonterminals of the resulting grammar.
(c) Construct the LL(1) table for the resulting grammar.
(d) Show the actions of the corresponding parser, given the following input string (a(b(2))(c)).

首先需要消除左递归、在第四行中lexp-seq -> lexp-seq lexp | lexp  这个存在递归、可以采用消除左递归的方式修改

简化一下一下。可以当做为 

X -> X A | A

那么就可以这样操作提取出A 再引入一个新的变量X’

X -> A X'
X'-> A X' 
     | ε

换到当前的这个例子中如下就变成了这样的

1: lexp -> atom | list
2: atom -> number | identifier
3: list -> (lexp-seq)
4: lexp-seq -> lexp seq2 
5: seq2 -> lexp seq2 
		 |  ε

所有的终结符：  number  identifier  （ ）

9.1 FIRST 集合

计算的过程如下 

FIRST(lexp)计算过程:
lexp -> atom,FIRST(atom) = {number, identifier}
lexp -> list,FIRST(list) = {(}
FIRST(lexp) = {number, identifier, (}

FIRST(atom)计算过程:
atom -> number,FIRST(number) = {number}
atom -> identifier，FIRST(identifier) = {identifier}
FIRST(atom) = {number, identifier}

FIRST(list)计算过程:
list -> ( lexp-seq ),FIRST(( ) = {(}
FIRST(list) = {(}

FIRST(lexp-seq)计算过程:
lexp-seq -> lexp seq2,FIRST(lexp) = {number, identifier, (}
FIRST(lexp-seq) = {number, identifier, (}

FIRST(seq2)计算过程:
seq2 -> lexp seq2,FIRST(lexp) = {number, identifier, (}
seq2 -> ε,FIRST(ε) = {ε}
FIRST(seq2) = {number, identifier, (, ε}

完整的FIRST集合 

FIRST(lexp)={number,identifier,(}
FIRST(atom)={number,identifier} 
FIRST(list) ={(}
FIRST(lexp-seq)={number,identifier,(}
FIRST(seq2)={number,identifier,(,ε}

最开始有点懵就是为什么FIRST(list) 没有 终结符 )  

解答： 

) 只可能出现在 list 的 结尾，而不是开头。在 list 的产生式 list -> ( lexp-seq ) 中，
) 是在 lexp-seq 之后才出现的。 FIRST 集合只关心 第一个 符号，因此 ) 
不会出现在任何一个非终结符的 FIRST 集合中

9.2 FOllow 集合


计算过程 

2. 计算 FOLLOW 集合

FOLLOW(S): 
	FOLLOW(S)={$}
	
FOLLOW(lexp):
将FOLLOW(S) 加入到FOLLOW(lexp)中 
lexp 出现在 lexp-seq -> lexp seq2 中，所以 FIRST(seq2) - {ε} 加入 FOLLOW(lexp)，即 {number, identifier, (} 加入。
lexp 出现在 seq2 -> lexp seq2 中，所以 FIRST(seq2) - {ε} 加入 FOLLOW(lexp)，即 {number, identifier, (} 加入。
lexp 出现在 list -> ( lexp-seq ) 中，所以 ) 加入 FOLLOW(lexp)。
FOLLOW(lexp) = {number, identifier, (, ),$}


FOLLOW(atom):
atom 出现在 lexp -> atom 中，所以 FOLLOW(lexp) 加入 FOLLOW(atom)。
FOLLOW(atom) = {number, identifier, (, ),$}

FOLLOW(list):
list 出现在 lexp -> list 中，所以 FOLLOW(lexp) 加入 FOLLOW(list)。
FOLLOW(list) = {number, identifier, (, ),$}

FOLLOW(lexp-seq):
lexp-seq 出现在 list -> ( lexp-seq ) 中，所以 ) 加入 FOLLOW(lexp-seq)。
FOLLOW(lexp-seq) = {)}

FOLLOW(seq2):
seq2 出现在 lexp-seq -> lexp seq2 中，所以 FOLLOW(lexp-seq) 加入 FOLLOW(seq2)。
FOLLOW(seq2) = {)}

说明一下为啥atom 需要加入FOLLOW(lexp) 
或者 list 为啥加入FOLLOW(list)
是因为 lexp -> list 后面是一个ε 根据规则需要加入 FOLLOW(A) 加入 FOLLOW(B)
得到的

得到所有的集合 

FOLLOW(lexp) = {number, identifier, (, ),$}
FOLLOW(atom) = {number, identifier, (, ),$}
FOLLOW(list) = {number, identifier, (, ),$}
FOLLOW(lexp-seq) = {)}
FOLLOW(seq2) = {)}

9.3 构造SELECT 集合

通过First 集合、Follow 集合

非终结符  First  Follow 

lexp

{number,identifier,(} {number, identifier, (, ),$}
atom {number,identifier}  {number, identifier, (, ),$}
list {(} {number, identifier, (, ),$}
lexp-seq {number,identifier,(} {)}
seq2 {number,identifier,(,ε}  {)}

SELECT 集合的定义分为两种情况：

  1. 如果 α 不能推导出 ε（空串）： SELECT(A → α) = FIRST(α)。也就是说，如果 α 不能推导出空串，那么其 SELECT 集合就是 α 的 FIRST 集合。

  2. 如果 α 可以推导出 ε（空串）： SELECT(A → α) = (FIRST(α) – {ε}) ∪ FOLLOW(A)。也就是说，如果 α 可以推导出空串，那么其 SELECT 集合是 α 的 FIRST 集合（去除 ε）和 A 的 FOLLOW 集合的并集。

SELECT 就如下： 

SELECT(S -> lexp $) = FIRST(lexp) = {number, identifier, (}
SELECT(lexp -> atom) = FIRST(atom) = {number, identifier}
SELECT(lexp -> list) = FIRST(list) = {(}
SELECT(list -> (lexp-seq)) = {(}
SELECT(lexp-seq -> lexp seq2) = FIRST(lexp) = {number, identifier, (}
SELECT(seq2 -> lexp seq2) = FIRST(lexp) = {number, identifier, (}
SELECT(seq2 -> ε) = FOLLOW(seq2) = {)}

这里需要注意的是，因为

seq2 -> lexp seq2 
|  ε
这里使用的| 所以需要分开进行计算所以就是两条。第一个是直接等于FIRST  第二条就需要根据规则 去掉ε 并FOLLOW 集

9.4 构造LL(1) 表

非终结符\终结符 number identifier ( ) $
S S -> lexp $ S -> lexp $ S -> lexp $
lexp lexp -> atom lexp -> atom lexp->list
atom atom -> number atom -> identifier
list list -> (lexp-seq)
lexp-seq     lexp-seq -> lexp seq2 lexp-seq -> lexp seq2 lexp-seq -> lexp seq2
seq2 seq2 -> lexp seq2 seq2 -> lexp seq2 seq2 -> lexp seq2 seq2 -> ε

9.5 输入(a(b(2))(c)) 的流程经过


步骤 栈 输入 动作
1 S$ (a(b(2))(c))$ S -> lexp $
2 lexp$ (a(b(2))(c))$ lexp -> list
3 list$ (a(b(2))(c))$ list -> (lexp-seq)
4 (lexp-seq)$ (a(b(2))(c))$ 匹配 (
5 lexp-seq)$ a(b(2))(c))$ lexp-seq -> lexp seq2
6 lexp seq2)$ a(b(2))(c))$ lexp -> atom
7 atom seq2)$ a(b(2))(c))$ atom -> identifier
8 identifier seq2)$ a(b(2))(c))$ 匹配 a
9 seq2)$ (b(2))(c))$ seq2 -> lexp seq2
10 lexp seq2)$ (b(2))(c))$ lexp -> list
11 list seq2)$ (b(2))(c))$ list -> (lexp-seq)
12 (lexp-seq seq2)$\$ (b(2))(c)) 匹配 (
13 lexp-seq seq2)$\$ b(2))(c)) lexp-seq -> lexp seq2
14 lexp seq2 seq2)$\$ b(2))(c)) lexp -> atom
15 atom seq2 seq2)$\$ b(2))(c)) atom -> identifier
16 identifier seq2 seq2)$\$ b(2))(c)) 匹配 b
17 seq2 seq2)$ (2))(c))$ seq2 -> lexp seq2
18 lexp seq2 seq2)$\$ (2))(c)) lexp -> atom
19 atom seq2 seq2)$\$ (2))(c)) atom -> number
20 number seq2 seq2)$\$ (2))(c)) 匹配 2
21 seq2 seq2)$ ))(c))$ seq2 -> ε
22 seq2)$ )(c))$ seq2 -> ε
23 )$ )(c))$ 匹配 )
24 $ (c))$ lexp ->list
25 list $ (c))$ list -> (lexp-seq)
26 (lexp-seq)$ (c))$ 匹配(
27 lexp-seq)$ c))$ lexp-seq -> lexp seq2
28 lexp seq2)$ c))$ lexp -> atom
29 atom seq2)$ c))$ atom -> identifier
30 identifier seq2)$ c))$ 匹配c
31 seq2)$ )$ seq2 -> ε
32 )$ )$ 匹配)
33 $ $ 接受

这里讲解一下具体的流程，

首先第一个( 会匹配到



如果觉得我的文章对您有用，请随意打赏。您的支持将鼓励我继续创作！

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注

更多阅读
标签云
Apache2.4.50 Apache ShenYu APISIX APISIX Dashboard cc5 CNVD-2021-49104 CNVD-2022-60632 CobaltStrike CobaltStrike xss CommonsCollections5 Confluence CVE-2021-26084 CVE-2017-18349 CVE-2021-4034 CVE-2021-37580 CVE-2021-41277 CVE-2021-41773 cve-2021-42013 CVE-2021-43798 CVE-2021-44228 CVE-2021-45232 CVE-2021-45232 RCE CVE-2022-22954 CVE-2022-22965 CVE-2022-39197 CVE-2023-28432 Django E-Office grafana keytool store log4j2 MetaBase ONE Access python python爬虫 socks5 socks5搜索 store 证书转换成nginx VMware Workspace ONE Access ysoserial 代理池工具 宝塔面板 泛微 畅捷通 畅捷通漏洞 通达OA